Use this Pythagorean theorem calculator to calculate the hypotenuse or the length of a right triangle’s missing leg. A right triangle’s hypotenuse is the side across the triangle’s right angle. You can find this side manually by performing a calculation with the hypotenuse formula which is also known as the Pythagorean theorem formula. Or you can use this hypotenuse calculator which is much easier.
Table of Contents
How to use the Pythagorean theorem calculator?
Using this Pythagorean calculator is an easy and convenient way to find the length of a right triangle or its hypotenuse. Follow these simple steps to use this online Pythagorean theorem solver:
- You only need to input two values which are the measurements of the right triangle’s legs that you have. Input value for (a) and a value for (b).
- After inputting these values, the Pythagorean theorem calculator will automatically generate the value for (c), the Area of the triangle, and its Perimeter.
How do you find the hypotenuse of a triangle?
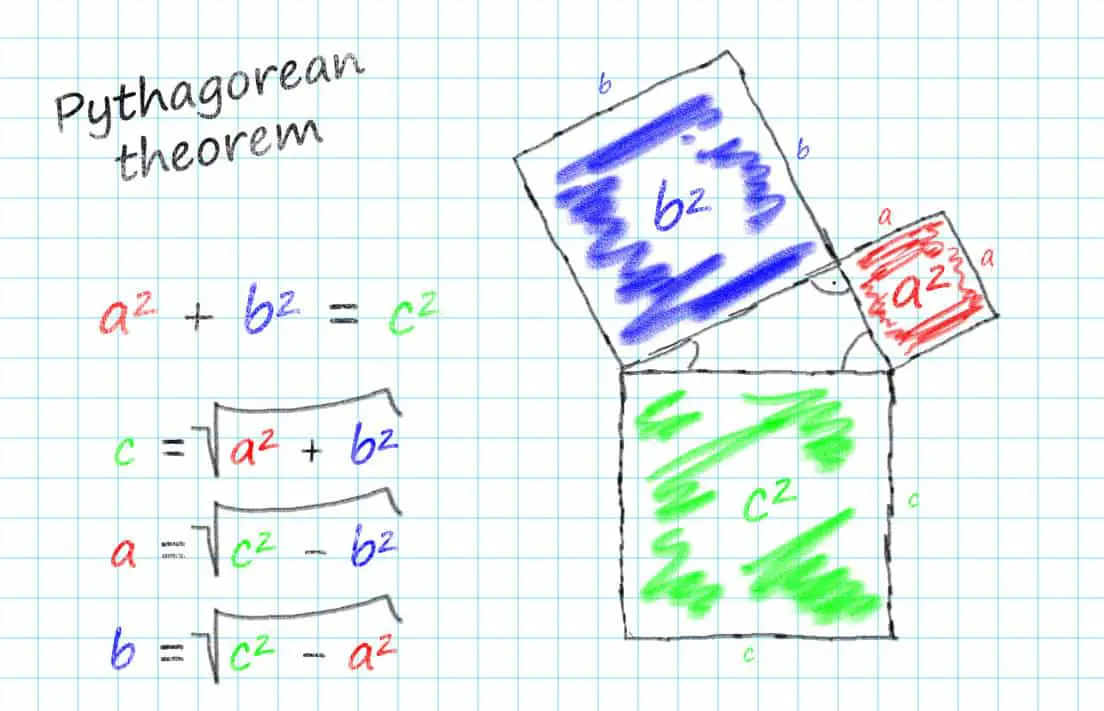
The main feature of a right triangle is that it should have one 90-degree angle. The hypotenuse refers to the side right across the right angle, and this side also happens to be the triangle’s longest side. Since the hypotenuse is the longest side, it’s easy to find by using various methods. You can use this Pythagorean calculator to find the hypotenuse, or you can follow these steps to perform the calculation manually:
- First, you need to learn about the Pythagorean theorem. This shows the relationship between right triangle’s sides. It states that any right triangle which has sides with lengths (a) and (b), the hypotenuse would have the length (c). Therefore, the Pythagorean theorem formula is a2 + b2 = c2.
- After understanding the theorem and the formula, the next step is to make sure that you’re working with a right triangle. The reason for this is that the Pythagorean theorem only applies to right triangles. Also, only right triangles possess a hypotenuse.
- Assign the variables (a), (b), and (c) to all the sides of your right triangle. Just keep in mind that you should only assign the variable (c) to the longest side of the triangle or the hypotenuse. Then you can assign the other variables to the other two sides of your triangle.
- The next step is to find the squares of the short sides which you’ve assigned with (a) and (b). Find these values by multiplying the numbers by themselves. After getting the values, place them into your formula.
- Going back to the original formula, add the squared values of (a) and (b) so that you can compute for the value of c2.
- Finally, compute for the square root of c2 by using a calculator’s square root function. The value you acquire is the length of the triangle’s hypotenuse.
When you look at a triangle, you’ll notice that all the sides would have a certain degree of slope or gradient. Therefore, you can also make use of a slope calculator if you want to calculate the slope of each of the triangle’s sides. If you have a right triangle, the sides which make up the right angle would possess slopes which, when multiplied would yield a product with a value of -1. If you want to calculate the slope manually, you can use this formula:
(y₂ – y₁)/(x₂ – x₁)
Let’s look at an example to illustrate this concept further. Let’s say that the right triangle had coordinates of (3,6) and (7,10). Using the formula above, you can plot the values:
(10 – 6) / (7 – 3) = 1/
If the other segment which forms the angle has a slope with a value of -1, this would mean that the lines are perpendicular. This is because:
1 * -1 = -1.
Therefore, this means that you have a right triangle.
If you don’t want to have to manually compute the missing lengths of a right triangle’s sides apart from the hypotenuse, then you can use a right triangle calculator. You can also make conversions using online tools. For instance, you have a problem which gives you values in degrees, and you want to convert these values to radians or vice versa, you can use an online angle converter. Again, you can convert these values manually by using these formulas:
- If the values of the angles are in radians: Multiply them by 180/π
- If the values of the angles are in degrees: Multiply them by π/180
There are also times when you get a problem where you’re missing two or all of the triangle’s side lengths. Unfortunately, this Pythagorean theorem calculator won’t be very helpful. In such cases, you would have to manually use the trigonometric functions so you can solve these missing lengths. You can calculate these values manually, or you can use a triangle calculator.
How Pythagoras prove his theorem?
The Pythagorean theorem is a type of relation which is typically utilized in Euclidean geometry, and it related to a right triangle’s three sides. This theorem states that the sum of the squares of all the right triangle’s sides equal the square of its hypotenuse. This is why the theorem is also known as the hypotenuse formula which is:
a² + b² = c²
The credit for this theorem foes to Pythagoras, the mathematician, and philosopher of ancient Greece. Although the Babylonians and Indians have already used this theorem, Pythagoras and his students were the first ones to prove this theorem. However, there’s no concrete proof that it was Pythagoras himself who proved the theorem named after him.
In any case, the proof credited to Pythagoras is extremely simple and is commonly known as the proof by rearrangement. Picture two squares and within them, picture four identical triangles. The only difference you would see between these two squares is the arrangement of the triangles within them. Therefore, this means that the space within the squares has an area that’s equal. Equating the area of this space would yield the Pythagorean theorem.
